Übersicht Produkte
Klinik
➜
Klinik
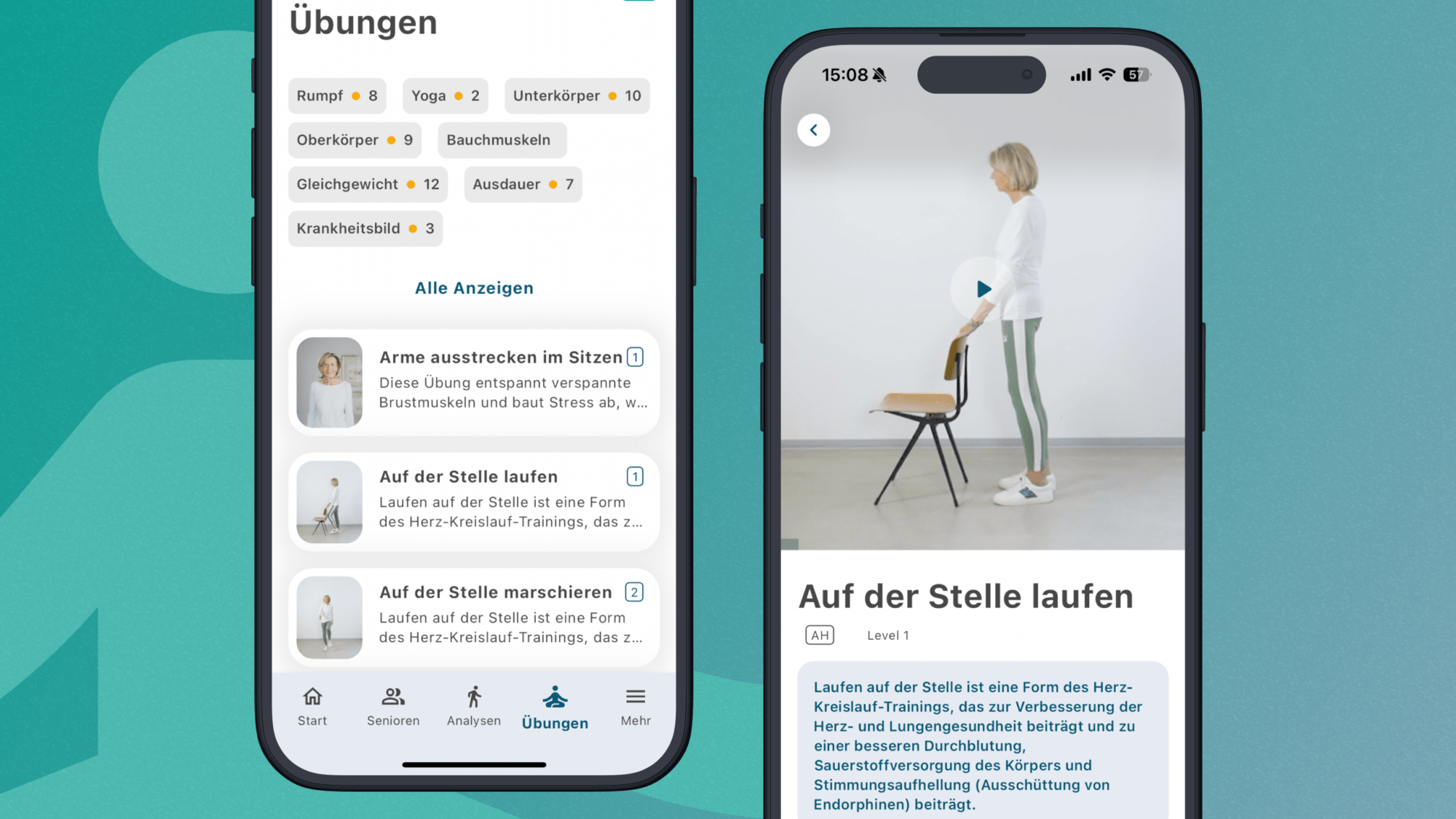
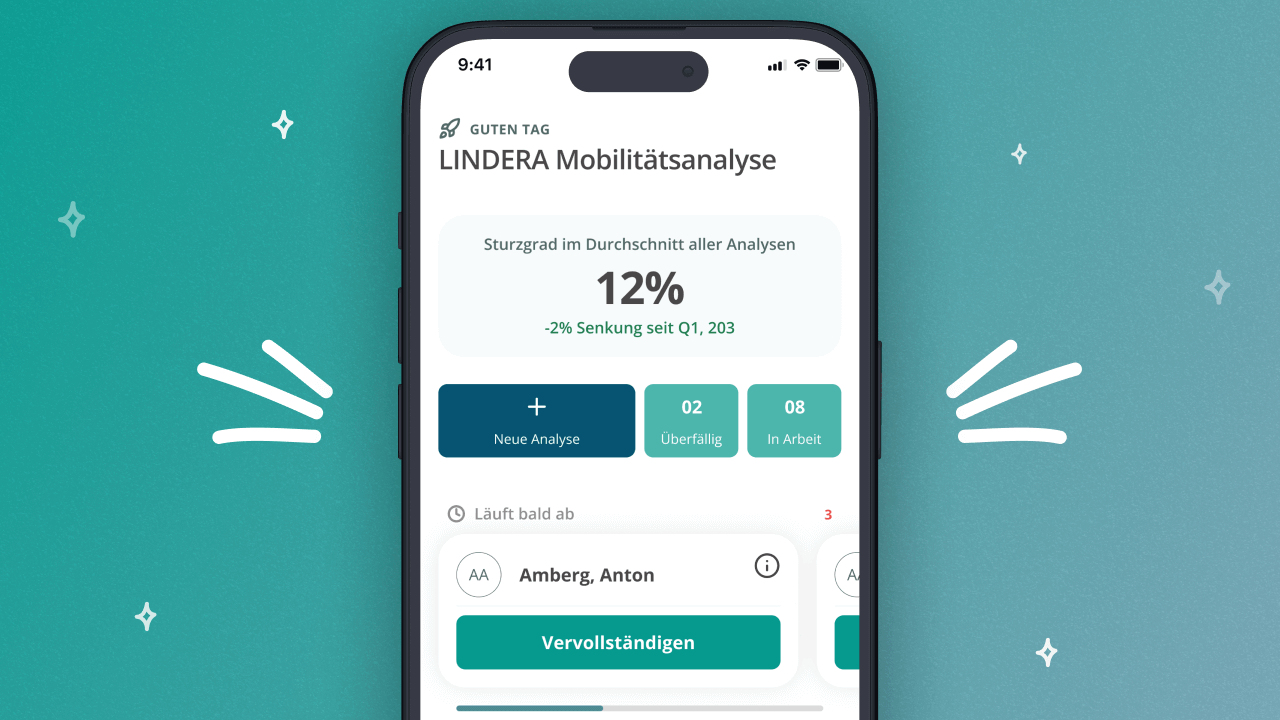
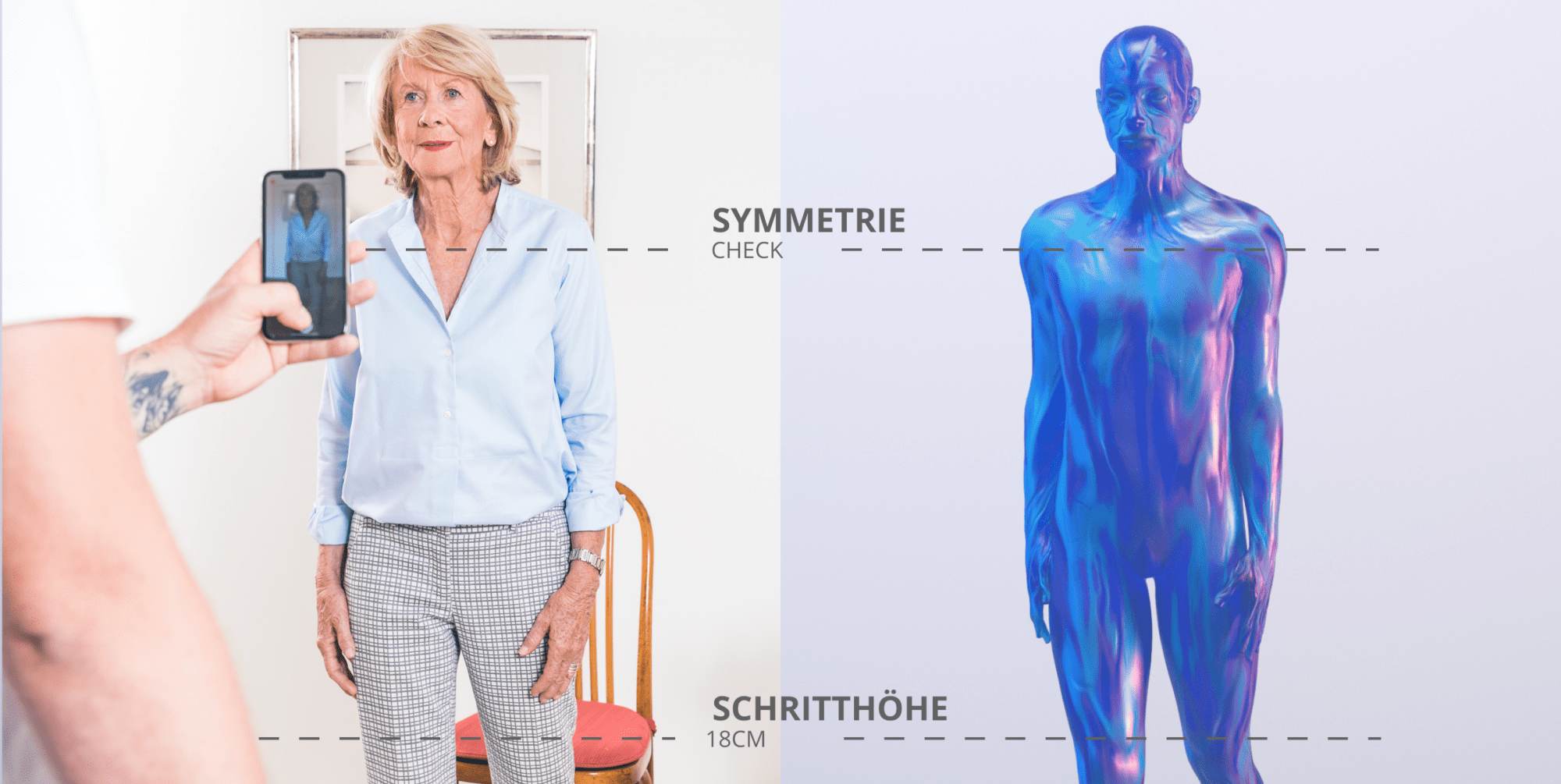
Die LINDERA KlinikApp ist das Schweizer Taschenmesser für alle Bereiche und Phasen des Klinikalltags. Aus einer einfachen Aufnahme per Smartphone-Kamera ermittelt unsere KI-Technologie das komplette 3D Skelett der Patient*innen – 21 Gelenkpunkte auf den Millimeter genau. Wozu? Wir messen genau die Bewegung, die ihnen Schmerzen bereitet, objektiv, nachvollziehbar, punktgenau. Entscheidungshilfe für Fachkräfte und Monitoring für Patient*innen – die KlinikApp begleitet Sie auf dem Weg zur Genesung!
In Kürze verfügbar
Tech
➜
Tech
Wie sieht personalisiertes Training in Zukunft aus? Für Entwickler*innen von Fitness- und Gesundheits-Apps hat LINDERA ein Tech Software Development Kit (SDK) released. App-Anbieter*innen integrieren die 3D-Motion Analyse in ihre mobile Anwendung. Dank des Algorithmus können sie Endkund*innen, wie Hobby- oder Profisportler*innen, ein personalisiertes Training mit Feedback in Echtzeit bieten – ganz ohne Multikamerasystem und Tiefensensorik.
Integration
Unsere Partner
Führende Krankenkassen und IT Anbieter für die Pflege- und Gesundheitsbranche gehören zu unseren Partnern.