Ein Blick in die Black Box – Teil 2 – Die Theorie des Informationsengpasses erneut betrachtet (Kurzfassung)

I. Einführung

Die Grundlagen der „Information-Bottleneck-Theorie“ (IB-Theorie) haben wir bereits in einem ersten Beitrag behandelt. Nun wollen wir noch tiefer in die IB-Theorie einsteigen. Dieser Blogpost ist dabei nur die kürzere, nicht-mathematische Version eines sehr viel ausführlicheren Beitrags, den ich schon vor einigen Wochen geschrieben habe. Es geht vor allem um zwei Themen: die Menge der verwendeten Trainingsdaten beim Deep Learning und welche Rolle die sogenannten Drift- und Diffusionsphasen für den Lernprozess spielen.

II. Die Rolle der Trainingsdaten – wie viel ist genug

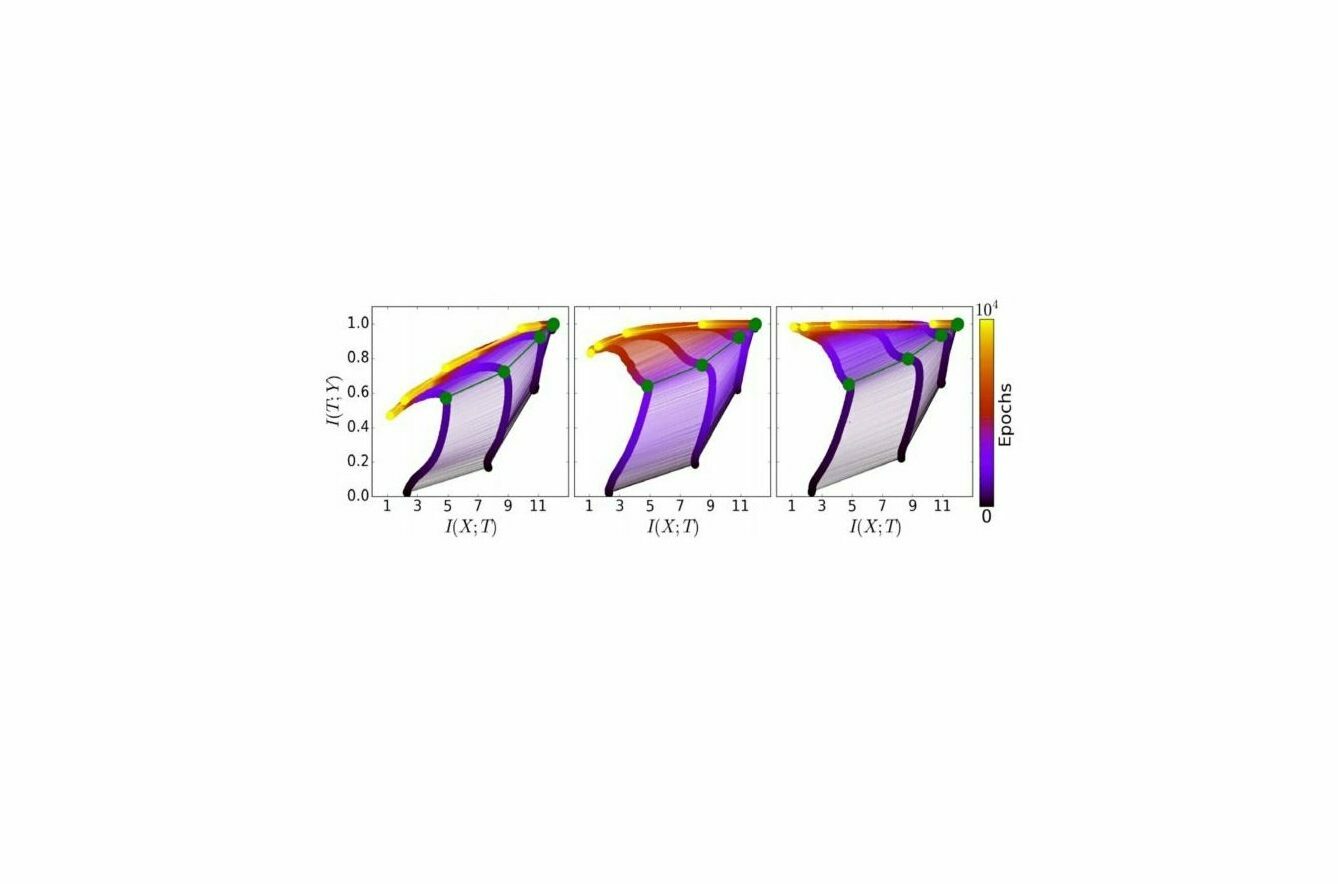
In unserer ersten Auseinandersetzung mit der IB-Theorie haben wir bereits gesehen, dass Deep Learning immer aus zwei Phasen besteht – der sogenannten Anpassungs- und der Kompressionsphase. Wir stellen das mit Hilfe eines zweidimensionalen Koordinatensystems dar (siehe Abbildung 1). Die Dynamik von unten bis zu der grünen Linie beschreibt die Anpassungsphase, während die darauffolgende Dynamik oberhalb der grünen Linie die Kompressionsphase beschreibt. Was wir nun grafisch in der Abbildung 1 sehen, ist – vereinfacht gesagt – die Trainingsdynamik der verschiedenen Ebenen eines neuronalen Netzwerks.

Ganz links ist diese Trainingsdynamik für ein künstliches neuronales Netz zu sehen, das fünf Prozent der Trainingsdaten verwendet. Das in der Mitte nutzt 45 Prozent, 85 Prozent sind es beim künstlichen neuronalen Netz rechts. Was ist zu sehen? Die Anpassungsphase auf der x-Achse ist in allen drei Fällen identisch. Die Veränderungen finden auf der y-Achse statt – also in der Kompressionsphase – deutlich zu sehen an der gelben Linie. Kleine Sätze von Trainingsdaten führen demnach also zu einer größeren Kompression – was ein Zeichen für eine Über-Anpassung ist. Die Kompression kann also zwar helfen, die Darstellung innerhalb der Schichten des künstlichen neuronalen Netzes zu vereinfachen – es muss aber stets die richtige Balance gefunden werden, damit relevante Informationen nicht verloren gehen.

III. Ein Gedankenexperiment – eine Exkursion in die statistische Mechanik

Lasst uns kurz über etwas anderes sprechen – wobei: Womöglich ist es das noch nicht einmal. Machen wir ein Gedankenexperiment.

III.1. Drift und Diffusion – Oder: die Farbe im Wasserglas

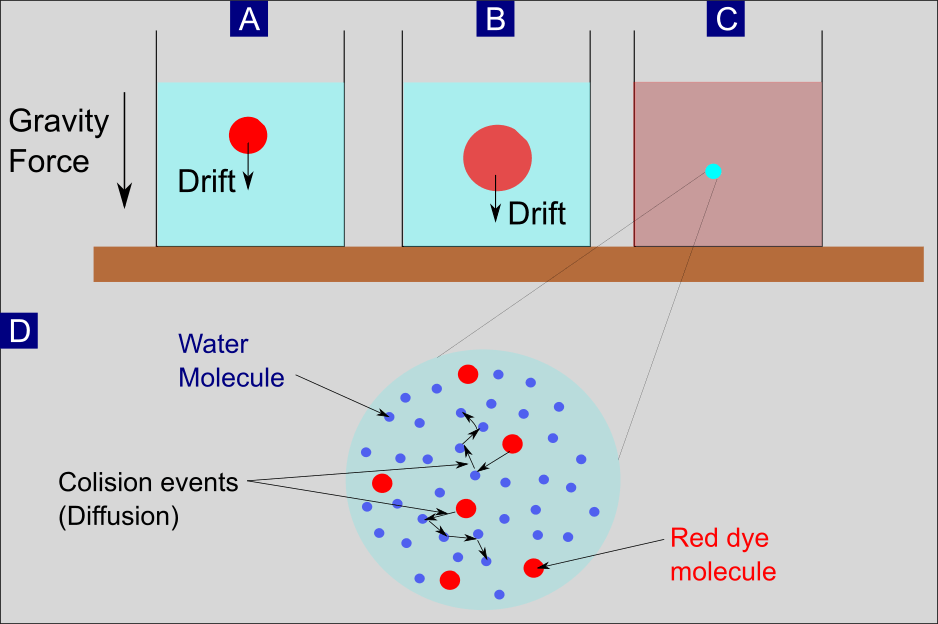
Wir nehmen ein Glas mit Wasser und geben einen Tropfen roter Farbe hinein. (Abbildung 2A). Was passiert?  Die Schwerkraft sorgt dafür, dass der Farbtropfen größtenteils erst einmal in Richtung Boden sinkt. In der Chemie ist hier vom Driften die Rede. Die sogenannte Diffusion wiederum sorgt dafür, dass der Farbtropfen an Volumen zunimmt (Abbildung 2B). Verantwortlich dafür ist die sogenannte Diffusion.  Das Zusammenspiel vom Driften und der Diffusion sorgt dafür, dass sich die Farbe gleichmäßig im Wasser verteilt. Je nach Menge der Farbe erscheint uns das Wasser insgesamt dann mehr oder weniger getrübt. Konkret haben sich die einzelnen Farbmoleküle gleichmäßig mit den Wassermolekülen gemischt.

III.2. Einzelne Partikel versus ein Zusammenspiel von Partikeln – die zwei Seiten derselben Medaille

Die Überlegung, die sich daran anschließt: Ist es, um die Prozesse zu verstehen, wichtiger, das Verhalten des einzelnen Farbmoleküls zu verstehen oder geht es um die Summe – also den Farbtropfen insgesamt? Das sind Fragen, um die es in der statistischen Mechanik geht. Sie befasst sich mit den Eigenschaften von Systemen, die sich aus vielen Teilen zusammensetzen – Gase und Flüssigkeiten sind hierfür typische Beispiele; und so auch unser Farbtropfen im Wasserglas. Ein anderes Beispiel haben wir im Gedankenexperiment mit dem Kaffeebecher im ersten Teil diskutiert.

Schon in der Römerzeit beschäftigten sich die großen Denker mit der Wechselwirkung vom Einzelnen mit der Summe, von Individuen und Gruppen. In seinem naturwissenschaftlichen Gedicht De rerum natura beschreibt der römische Dichter und Philosoph Lucretius schon im ersten Jahrhundert v. Chr. ein Phänomen, das heute als Brownsche Bewegung bekannt ist: die unregelmäßige Bewegung von kleinen Teilen in einer Flüssigkeit. Lucretius‘ selbst führte die zufälligen Bewegungen auf die Kollision mit Luftmolekülen zurück, was für ihn auch der Beweis war, dass Atome existieren.

Neben einem zufälligen Teil der Bewegung beschrieb Lucretius‘ auch jenen, der sich durch die Anwendung der Naturgesetze vorhersagen lässt. In seinem Staubkorn-Beispiel sind das die Luftströme, die die Staubmoleküle bewegen. In unserem Gedankenexperiment entspricht das dem Absinken des Farbtropfens im Wasserglas, also der Drift-Bewegung.

III.3. Die Einzelteilchen-Perspektive – Stochastische Differentialgleichungen

Doch zurück zur Brownschen Bewegung. Benannt wurde sie nach dem schottischen Botaniker Robert Brown.

Eine stochastische Differentialgleichung (SDG) beschreibt bei der Brownschen Bewegung die Dynamik der einzelnen Partikel. Mit Hilfe der Gleichung ist es möglich zu simulieren, wie sich Tausende oder Millionen von Partikel in einer Lösung – beispielsweise mit Wasser – bewegen. Die Gleichung arbeitet mit einer speziellen Form der Wahrscheinlichkeitsrechnung. Am Anfang können die größeren Partikel in einem kleinen Bereich des Wassers noch konzentriert sein (wie in Abbildung 1). Im weiteren Verlauf weichen die Bewegungen der einzelnen Partikel jedoch immer stärker voneinander ab – da die SDG für jedes Partikel einen anderen Bewegungsablauf ergibt. Um nun beispielsweise die Verteilung des Farbtropfens im Wasser abzubilden, ist es notwendig, ganz viele SDG zu berücksichtigen. Möglich macht das die sogenannte Monte-Carlo-Simulation.

III.4. Eine zusammenfassende Beschreibung – die Fokker-Planck-Gleichung

Bislang haben wir uns damit aber immer noch auf der Ebene der einzelnen Partikel bewegt, die sich im Wasser verteilen. Doch was passiert, wenn wir von dieser mikroskopischen auf eine makroskopische Ebene wechseln? Dann verwischen die einzelnen Partikel – und auch die mathematische Beschreibung ändert sich. Statt mit Millionen von einzelnen SDG haben wir es nur noch mit einer einzigen Gleichung zu tun, die auch als Fokker-Planck-Gleichung bezeichnet wird.

Die Fokker-Planck-Gleichung wurde erstmals von dem niederländischen Physiker und Musiker Adriaan Fokker und dem berühmten deutschen Physiker Max Planck aufgestellt, um die Brownsche Bewegung aus einer zusammenfassenden Perspektive zu beschreiben. Sie ist aber auch als Kolmogorov-Vorwärtsgleichung bekannt und geht auf den russischen Mathematiker Andrey Kolmogorov zurück. Er entwickelte die Gleichung 1931 unabhängig von Fokker und Planck. 

Worauf es an dieser Stelle ankommt: Obwohl der Bewegungsablauf für jedes einzelne Partikel zufällig ist, wie wir zuvor gesehen haben, entwickelt sich die Summe der Teilchen deterministisch – sie ist also berechen-, das heißt vorhersagbar. Um unser Beispiel von weiter oben aufzugreifen: Die einzelnen Farbpartikel mögen sich zufällig bewegen, wir können aber dennoch verlässliche Vorhersagen für das Gesamtsystem machen.

III.5. Die Fokker-Planck-Gleichung als Kontinuitätsgleichung

Es gibt eine optisch ansprechende Neuformulierung der Fokker-Planck-Gleichung in der Form einer Kontinuitätsgleichung. Ohne hier groß auf die Details eingehen zu wollen: Wir können die Kontinuitätsgleichung leicht durch ein schematisches Bild wie in Abbildung 4 veranschaulichen.

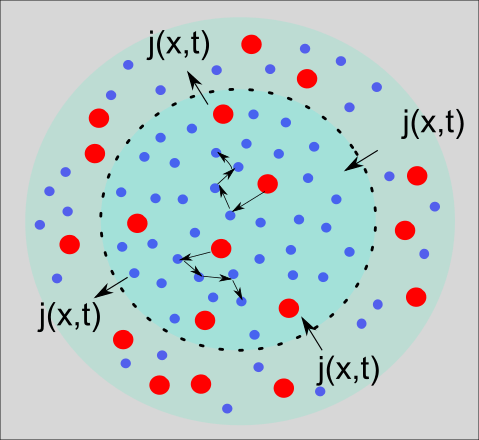
Wir sehen erneut eine Diffusion. Farbpartikel bewegen sich zufällig in einer Flüssigkeit umher. In der Darstellung sehen wir außerdem eine schwarze gestrichelte Linie, die einen inneren von einem äußeren Kreis voneinander trennt. Die Dichte der roten Farbpartikel im inneren Kreis verändert sich über die Zeit, weil einige der Partikel die gestrichelte Linie passieren (von innen nach außen und umgekehrt). Die einzelnen Partikel bewegen sich zufällig, wir können aber dennoch über die Kontinuitätsgleichung Aussagen darüber machen, wie sich die Dichte im Verhältnis zum Faktor Zeit verändert. 

V. Zusammenfassung und Ausblick

Nun stellt sich die Frage: Wie helfen uns diese Details zur Drift- und Diffusionsphase dabei, Deep Learning besser zu verstehen? Die Antwort liegt darin, dass sie gleichzusetzen sind mit der Anpassungs- und Kompressionsphase, die wir beim Training neuronaler Netze haben.

In diesem Beitrag haben wir gesehen, welche Rolle die Menge an Trainingsdaten für das endgültige Trainingsergebnis hat. Zwar hat die Menge an Daten keinen Einfluss auf die Anpassungsphase, sie nimmt aber eine Schlüsselrolle für die Kompressionsphase ein. Eine zu geringe Menge an Trainingsdaten führt zu einer Überkomprimierung von Informationen.

Außerdem haben wir herausgearbeitet, wie die beiden Phasen beim Deep Learning mit den Drift- und Diffusionstermini der Fokker-Planck-Gleichung (FP) übereinstimmen. Die FP-Gleichung ist in der statistischen Mechanik weit verbreitet. Dies wurde insbesondere im Zusammenhang mit der Brownschen Bewegung größerer Teilchen in einer Flüssigkeit veranschaulicht.

Im dritten Teil werden wir uns mit der Rolle der versteckten Schichten beschäftigten, die für neuronale Netzwerke eine hohe Relevanz haben. Es wird vor allem um die Frage gehen, welchen Einfluss die versteckten Schichten auf die Trainingszeit haben. Außerdem werden wir uns mit einigen Unzulänglichkeiten der IB-Theorie befassen und versuchen, Lösungen und Alternativen anzubieten.